Example #2

Introduction

Compare models with the data set ‘math’. Apart from the regular flow from DF, sections have been added on data set understanding together with a delve into regular GLM (General not Generalized!) and some funky visualizations of multi-factorial models.

Example #2

require(flexplot)

Loading required package: flexplot

require(lme4)

Loading required package: lme4

Loading required package: Matrix

require(dplyr)

Loading required package: dplyr

Attaching package: 'dplyr'

The following objects are masked from 'package:stats':

    filter, lag

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

require(ggplot2)

Loading required package: ggplot2

Attaching package: 'ggplot2'

The following object is masked from 'package:flexplot':

    flip_data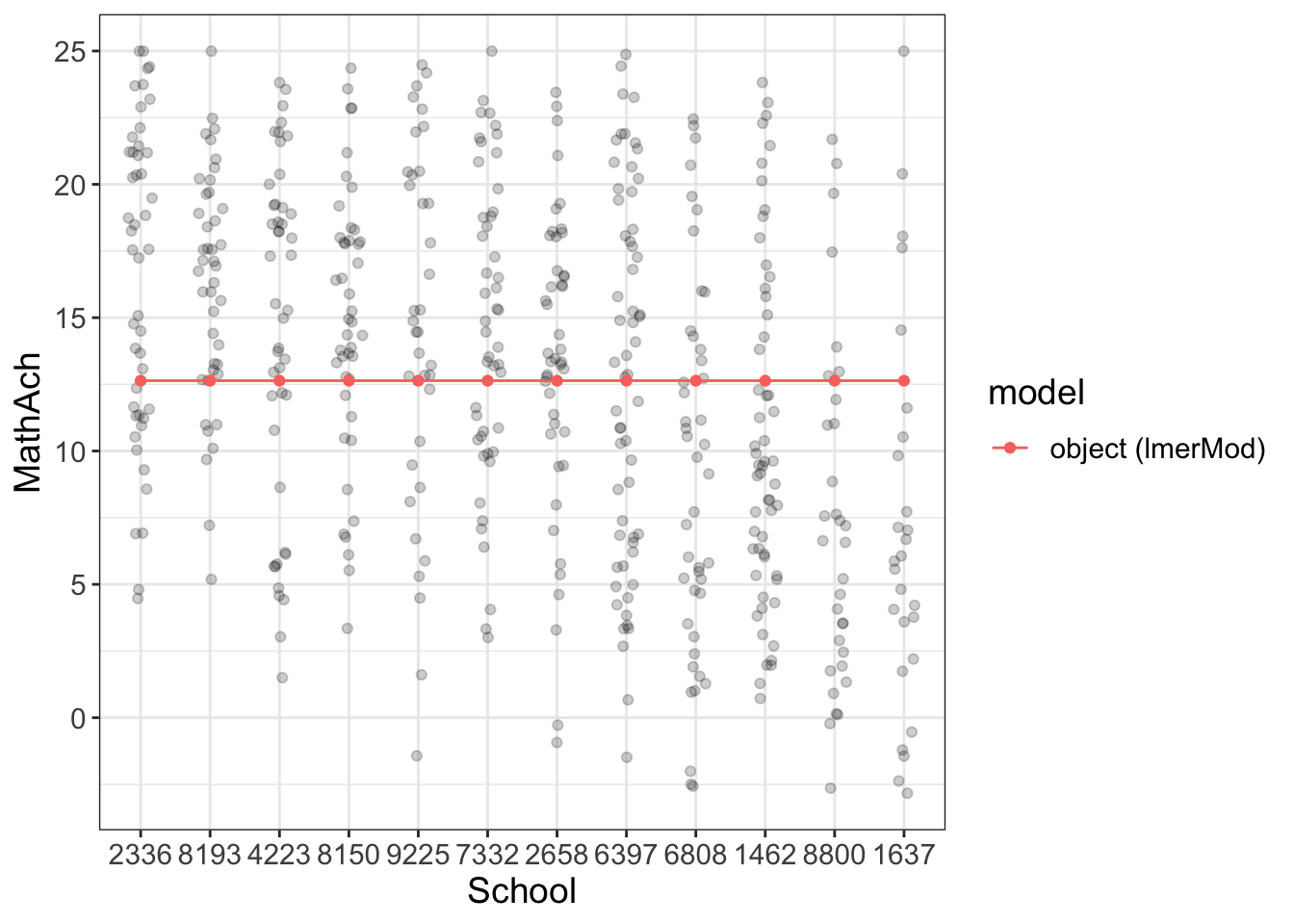

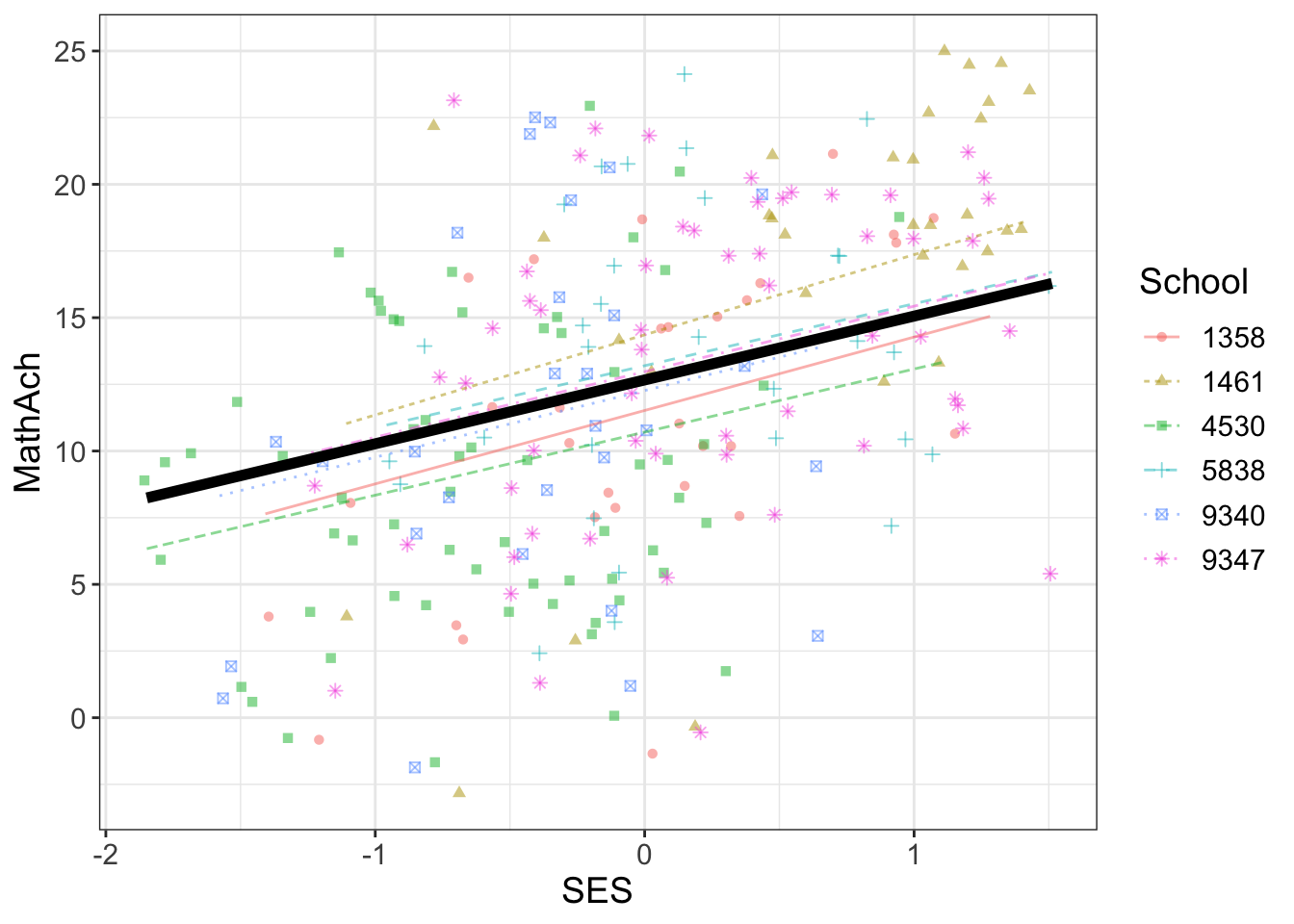
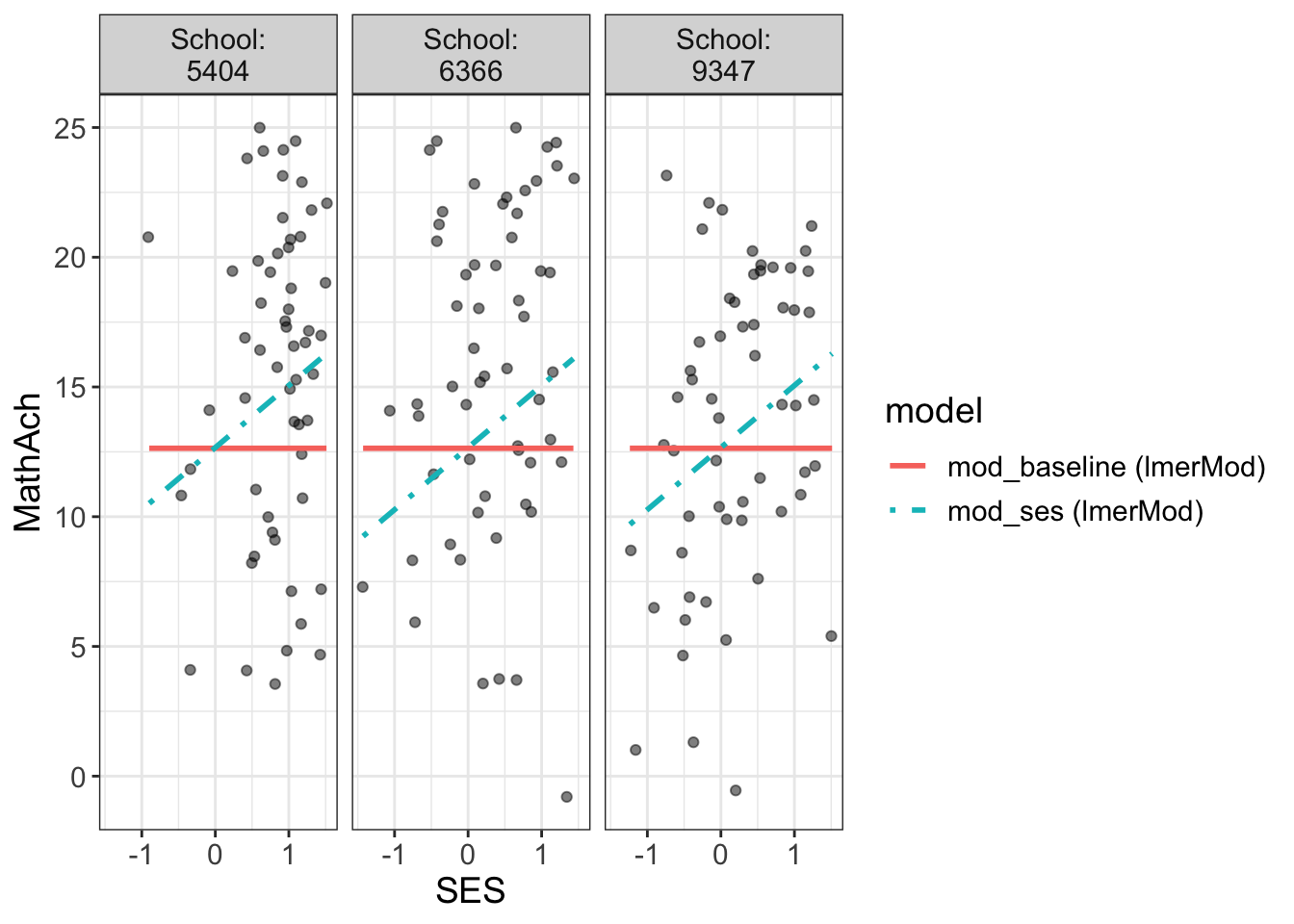
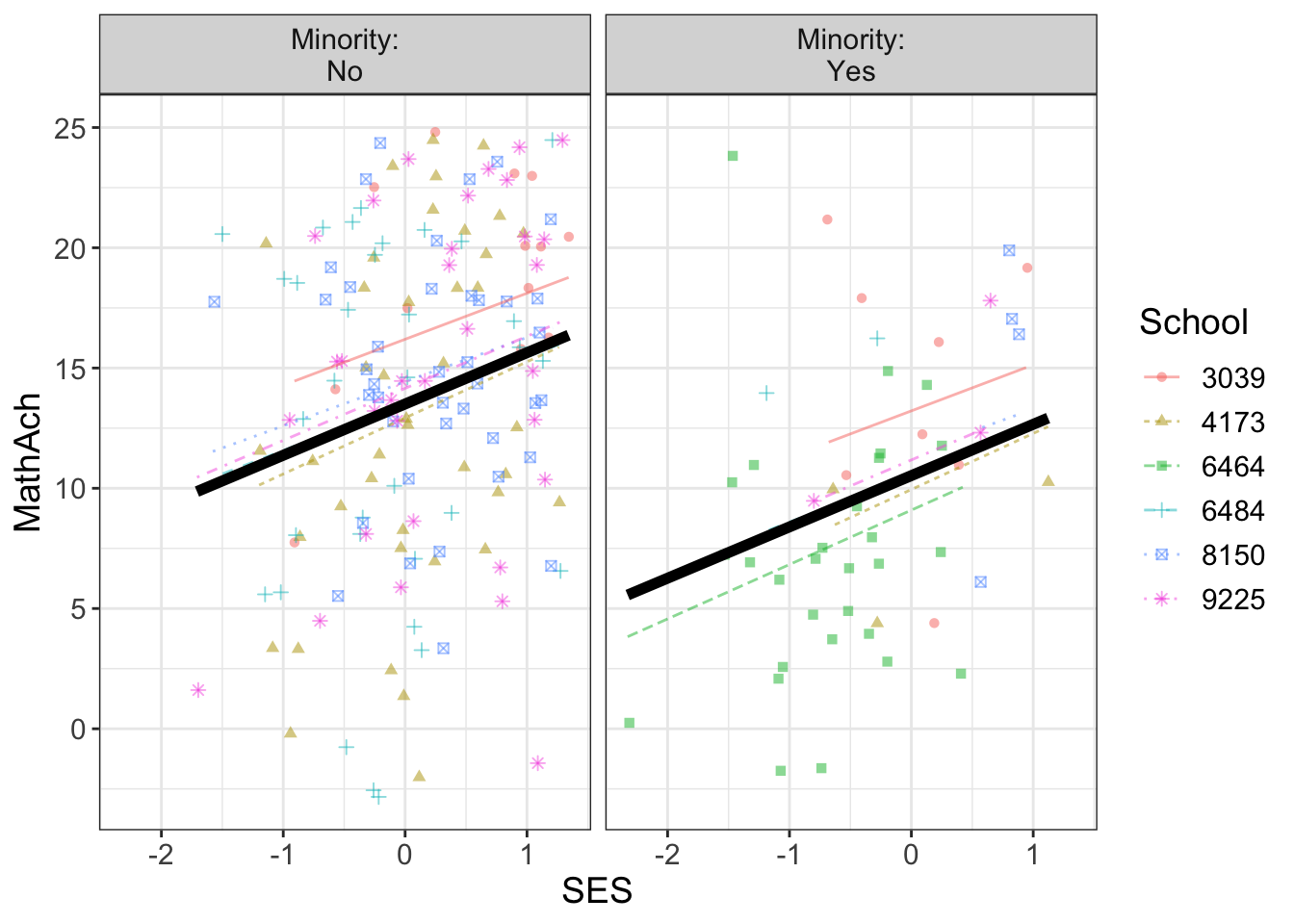
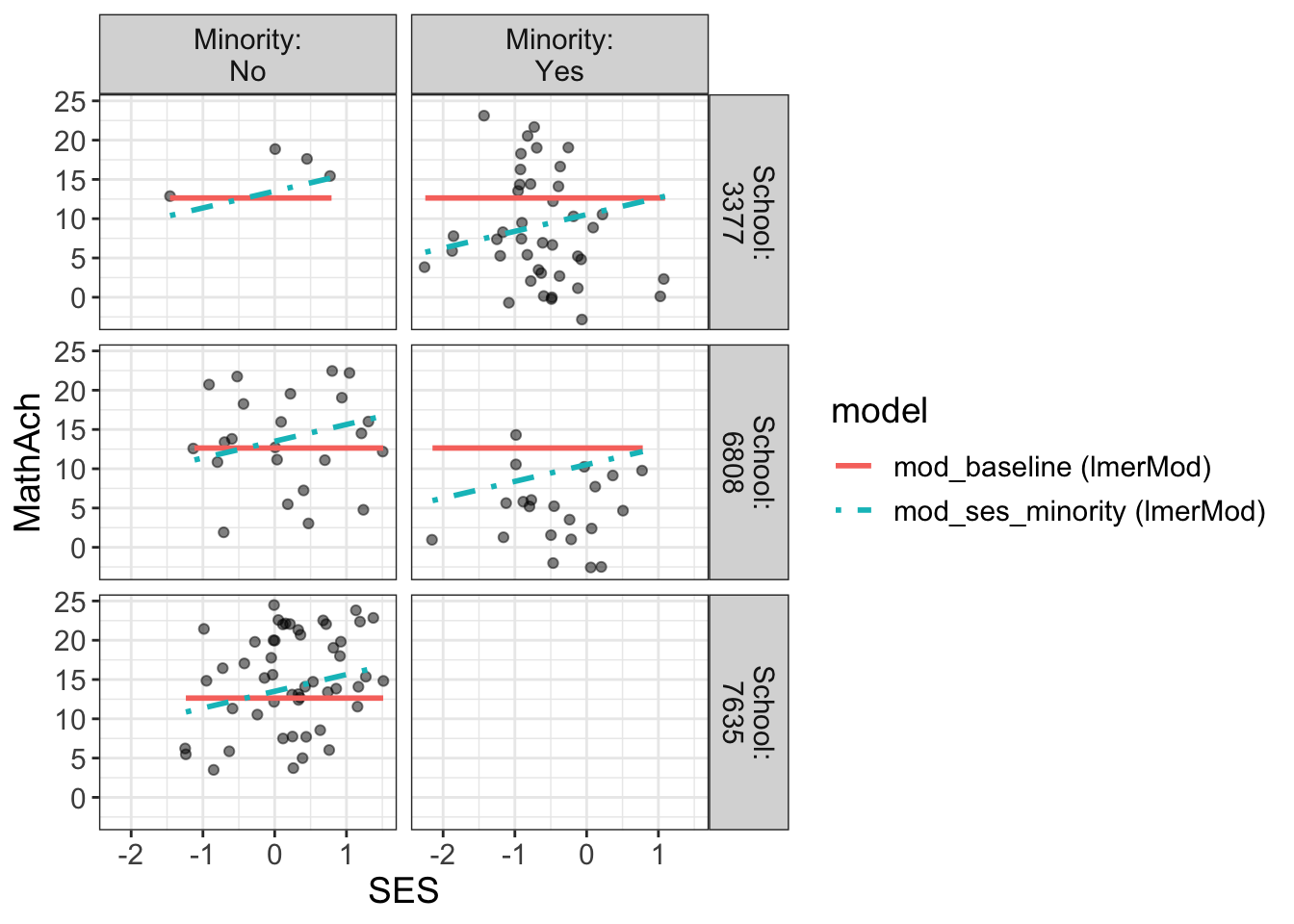
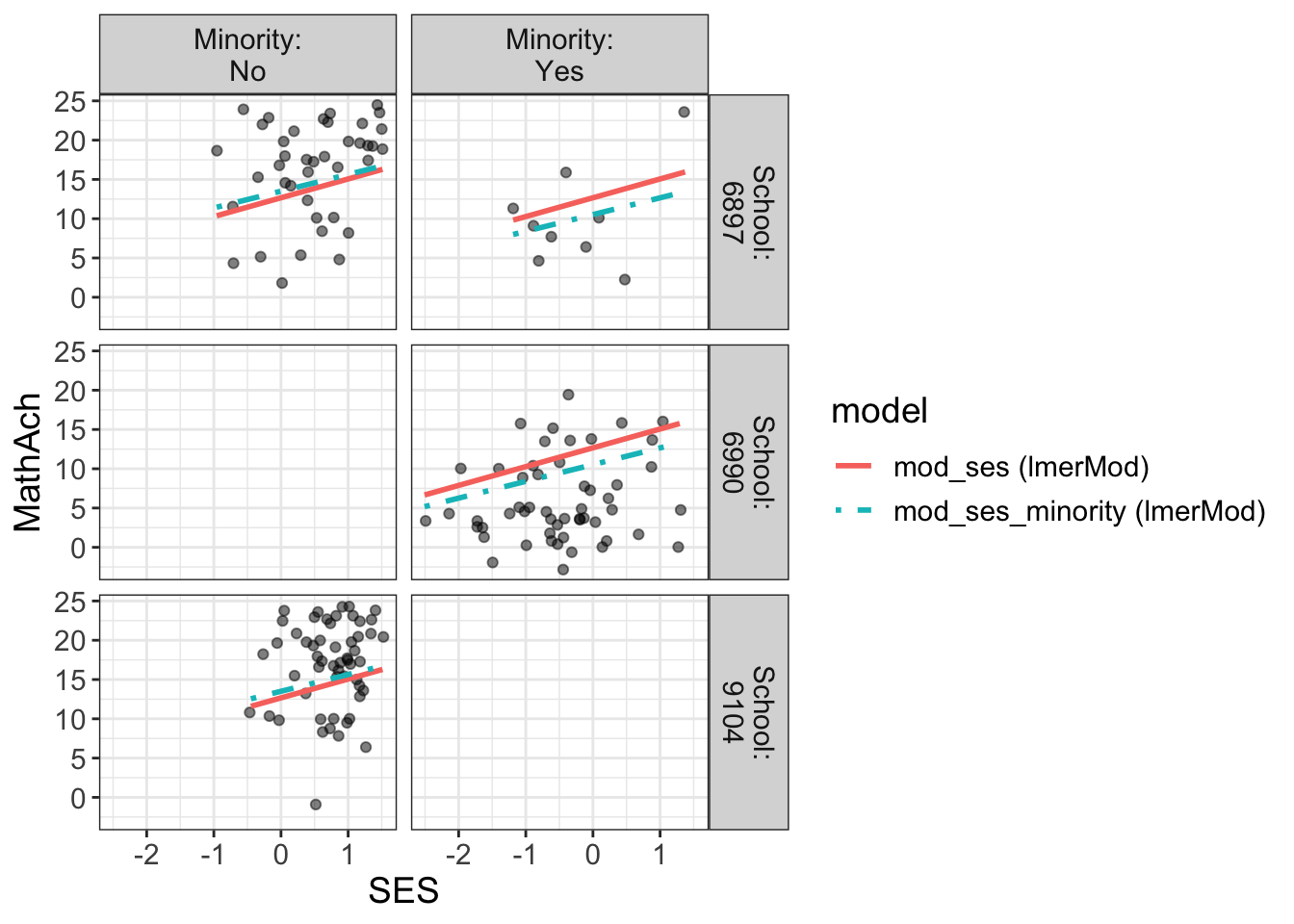
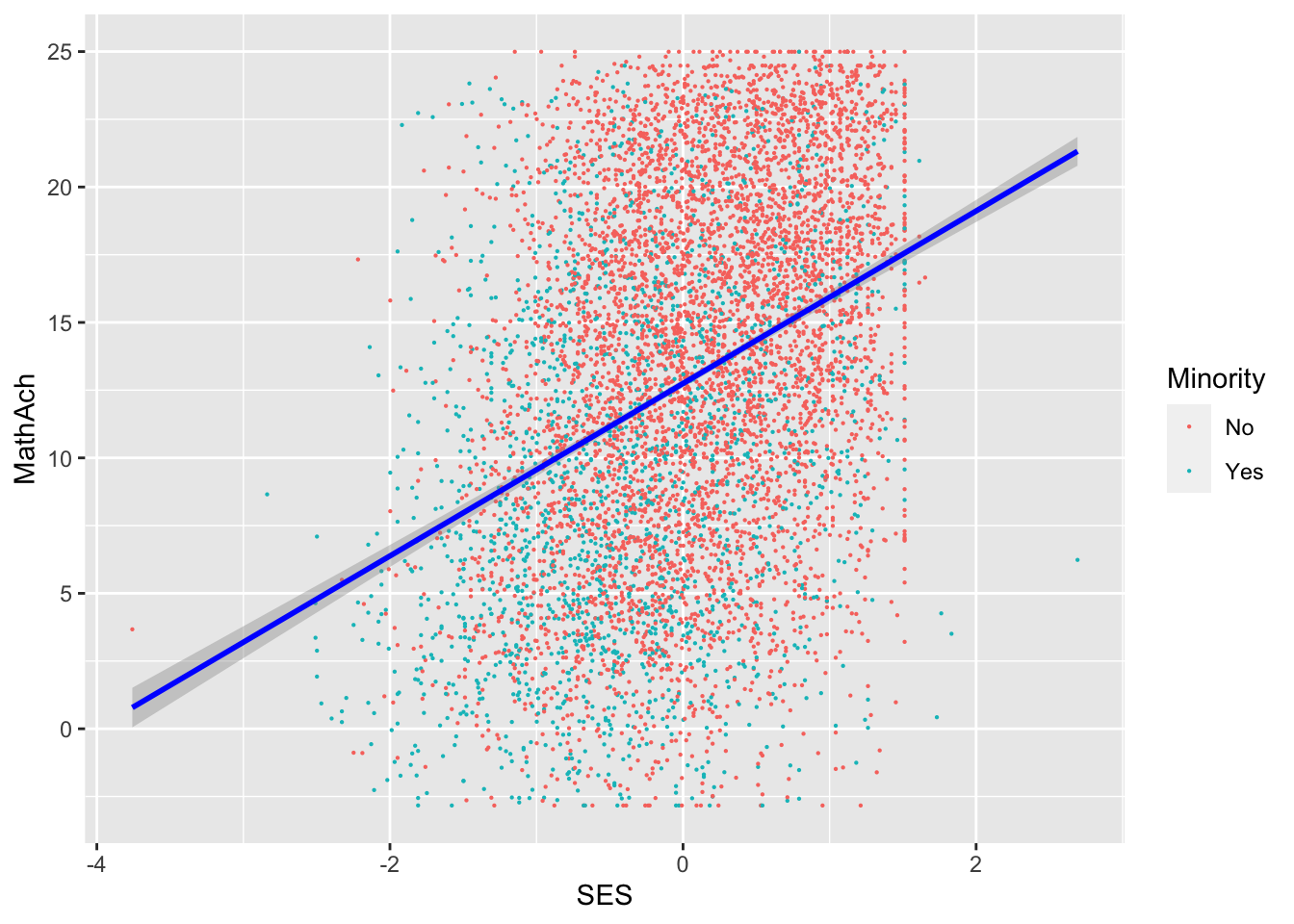
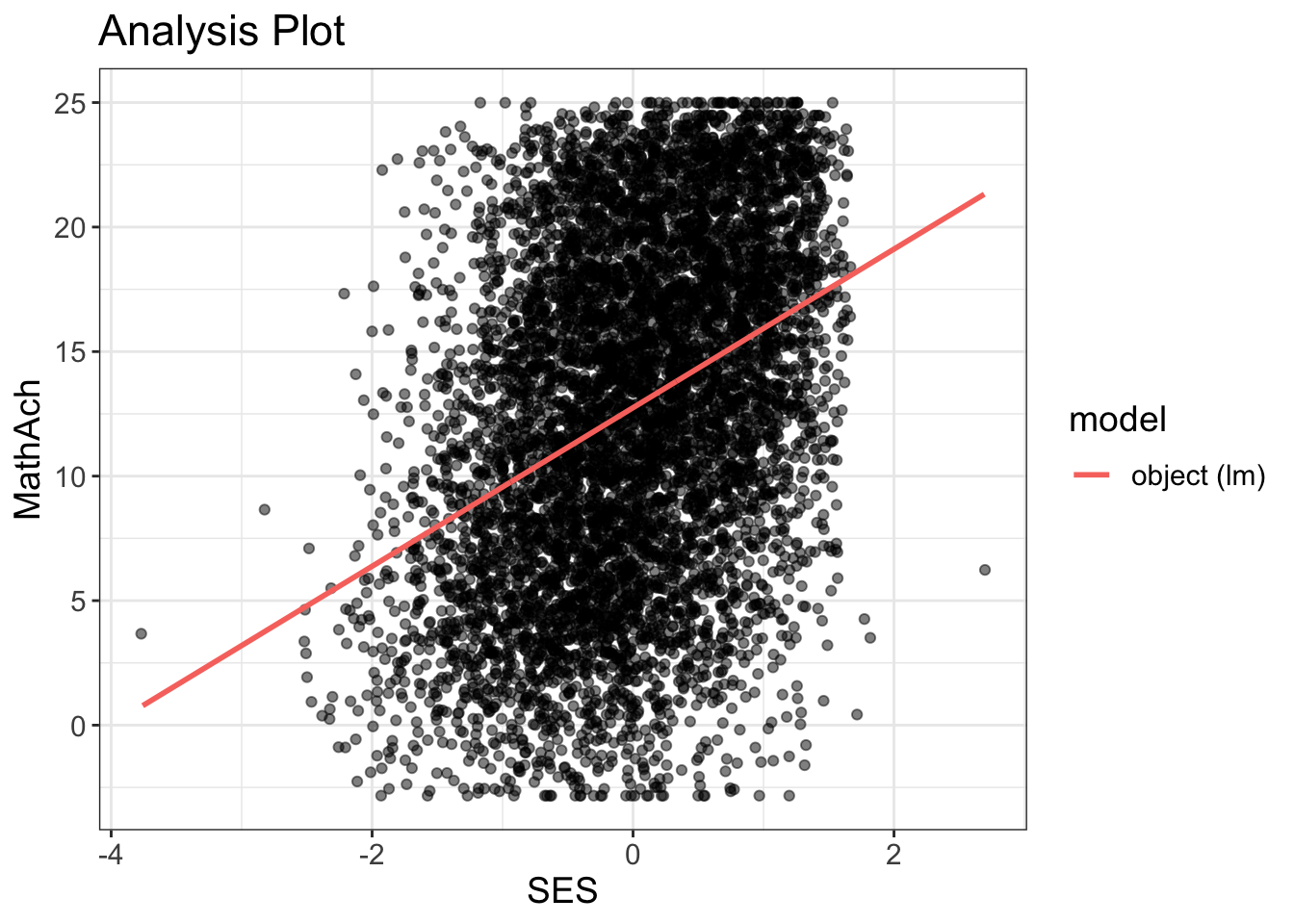
First look at the data

data(math)
head(math,10)

   School Minority    Sex    SES MathAch MEANSES
1    1224       No Female -1.528   5.876  -0.428
2    1224       No Female -0.588  19.708  -0.428
3    1224       No   Male -0.528  20.349  -0.428
4    1224       No   Male -0.668   8.781  -0.428
5    1224       No   Male -0.158  17.898  -0.428
6    1224       No   Male  0.022   4.583  -0.428
7    1224       No Female -0.618  -2.832  -0.428
8    1224       No   Male -0.998   0.523  -0.428
9    1224       No Female -0.888   1.527  -0.428
10   1224       No   Male -0.458  21.521  -0.428

glimpse(math)

Rows: 7,185
Columns: 6
$ School   <int> 1224, 1224, 1224, 1224, 1224, 1224, 1224, 1224, 1224, 1224, 1…
$ Minority <fct> No, No, No, No, No, No, No, No, No, No, No, No, No, No, No, N…
$ Sex      <fct> Female, Female, Male, Male, Male, Male, Female, Male, Female,…
$ SES      <dbl> -1.528, -0.588, -0.528, -0.668, -0.158, 0.022, -0.618, -0.998…
$ MathAch  <dbl> 5.876, 19.708, 20.349, 8.781, 17.898, 4.583, -2.832, 0.523, 1…
$ MEANSES  <dbl> -0.428, -0.428, -0.428, -0.428, -0.428, -0.428, -0.428, -0.42…

math %>% group_by(Minority, Sex) %>% summarise(.groups = "keep")

# A tibble: 4 × 2
# Groups:   Minority, Sex [4]
  Minority Sex   
  <fct>    <fct> 
1 No       Female
2 No       Male  
3 Yes      Female
4 Yes      Male  

math %>% group_by(School) %>% summarise(.groups = "keep")

# A tibble: 160 × 1
# Groups:   School [160]
   School
    <int>
 1   1224
 2   1288
 3   1296
 4   1308
 5   1317
 6   1358
 7   1374
 8   1433
 9   1436
10   1461
# ℹ 150 more rows

summary(math)

     School     Minority       Sex            SES               MathAch      
 Min.   :1224   No :5211   Female:3795   Min.   :-3.758000   Min.   :-2.832  
 1st Qu.:3020   Yes:1974   Male  :3390   1st Qu.:-0.538000   1st Qu.: 7.275  
 Median :5192                            Median : 0.002000   Median :13.131  
 Mean   :5278                            Mean   : 0.000143   Mean   :12.748  
 3rd Qu.:7342                            3rd Qu.: 0.602000   3rd Qu.:18.317  
 Max.   :9586                            Max.   : 2.692000   Max.   :24.993  
    MEANSES         
 Min.   :-1.188000  
 1st Qu.:-0.317000  
 Median : 0.038000  
 Mean   : 0.006138  
 3rd Qu.: 0.333000  
 Max.   : 0.831000  

Comments

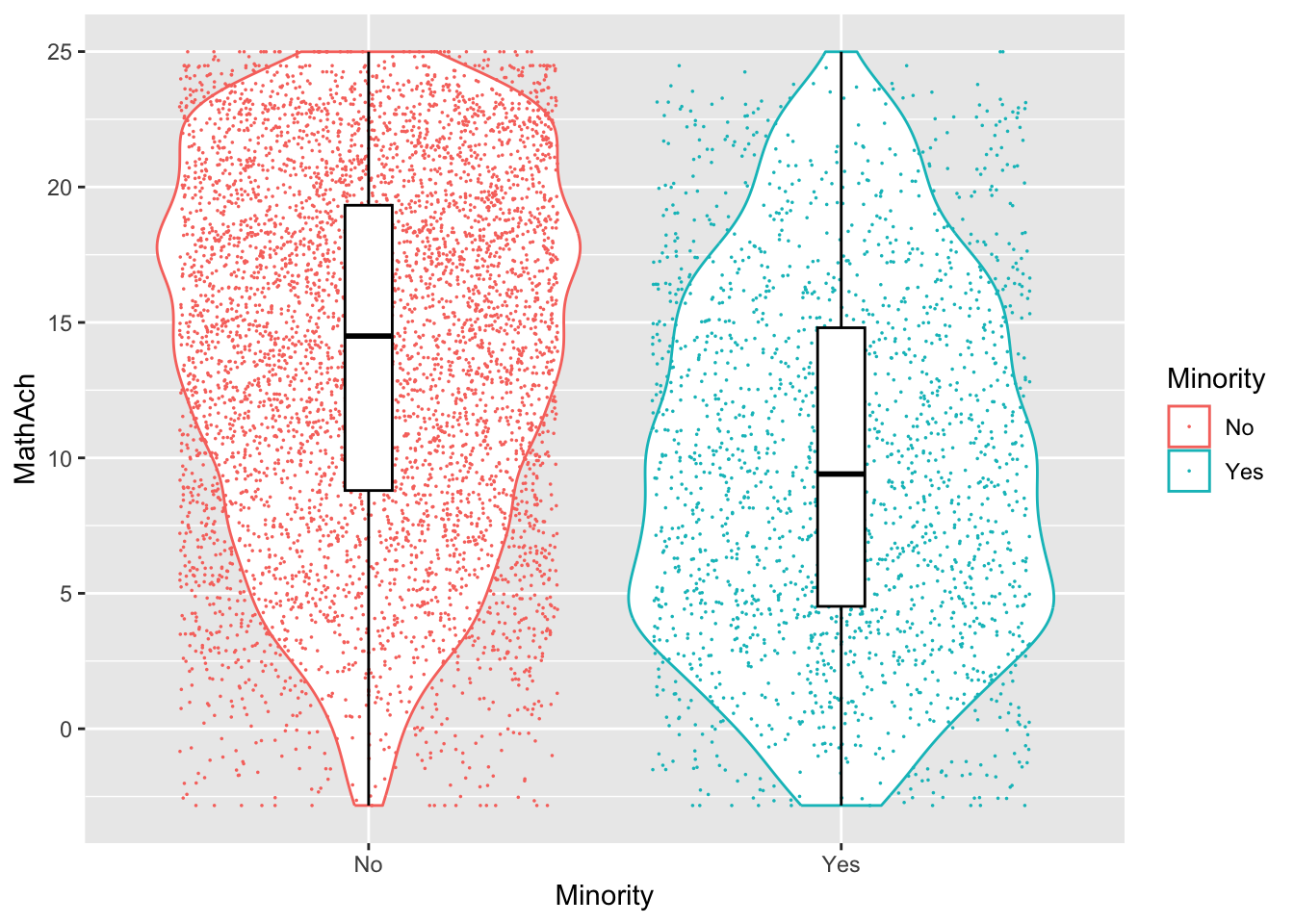
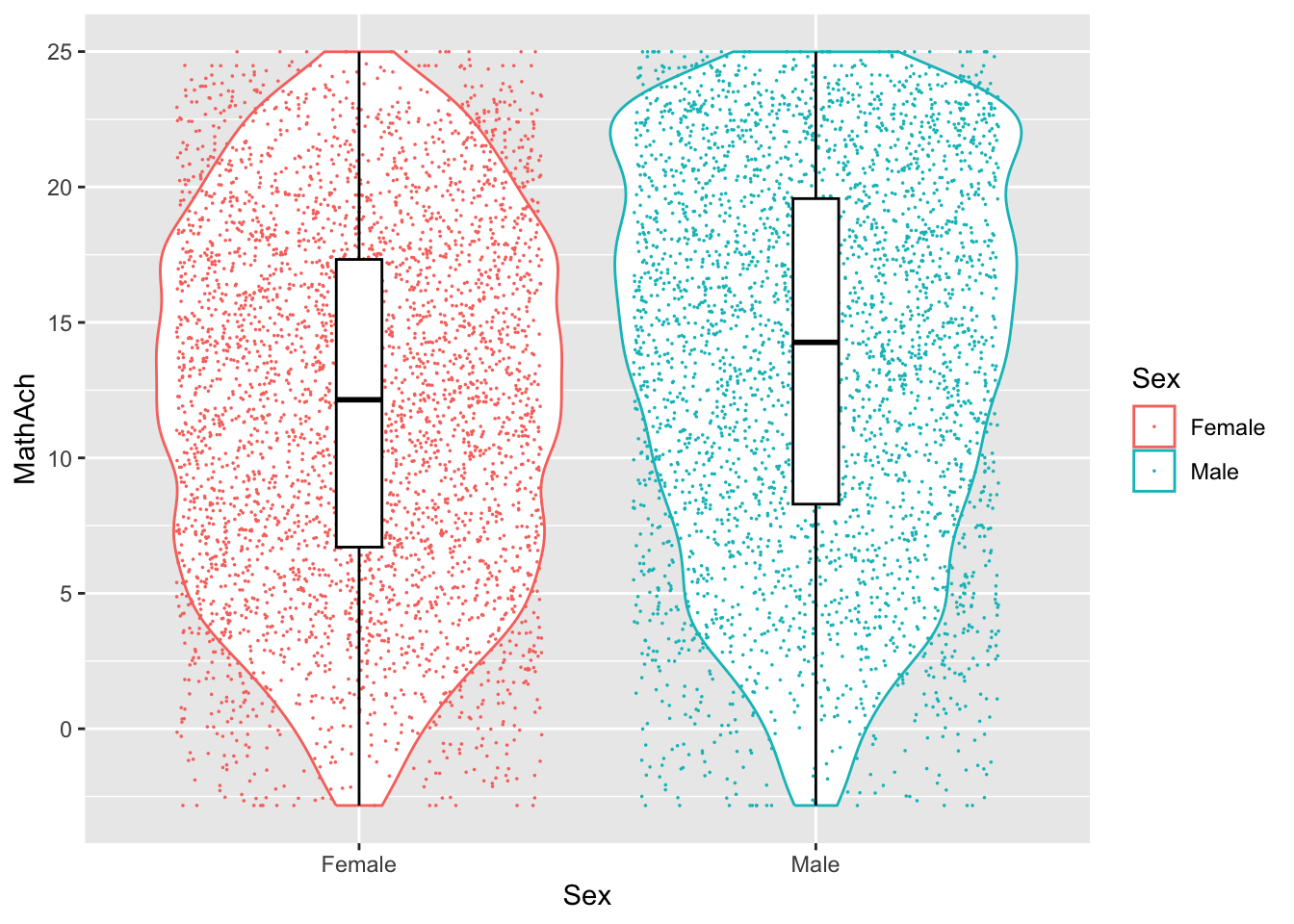
• From the above, we have 160 schools with two genders classified as minority or not.

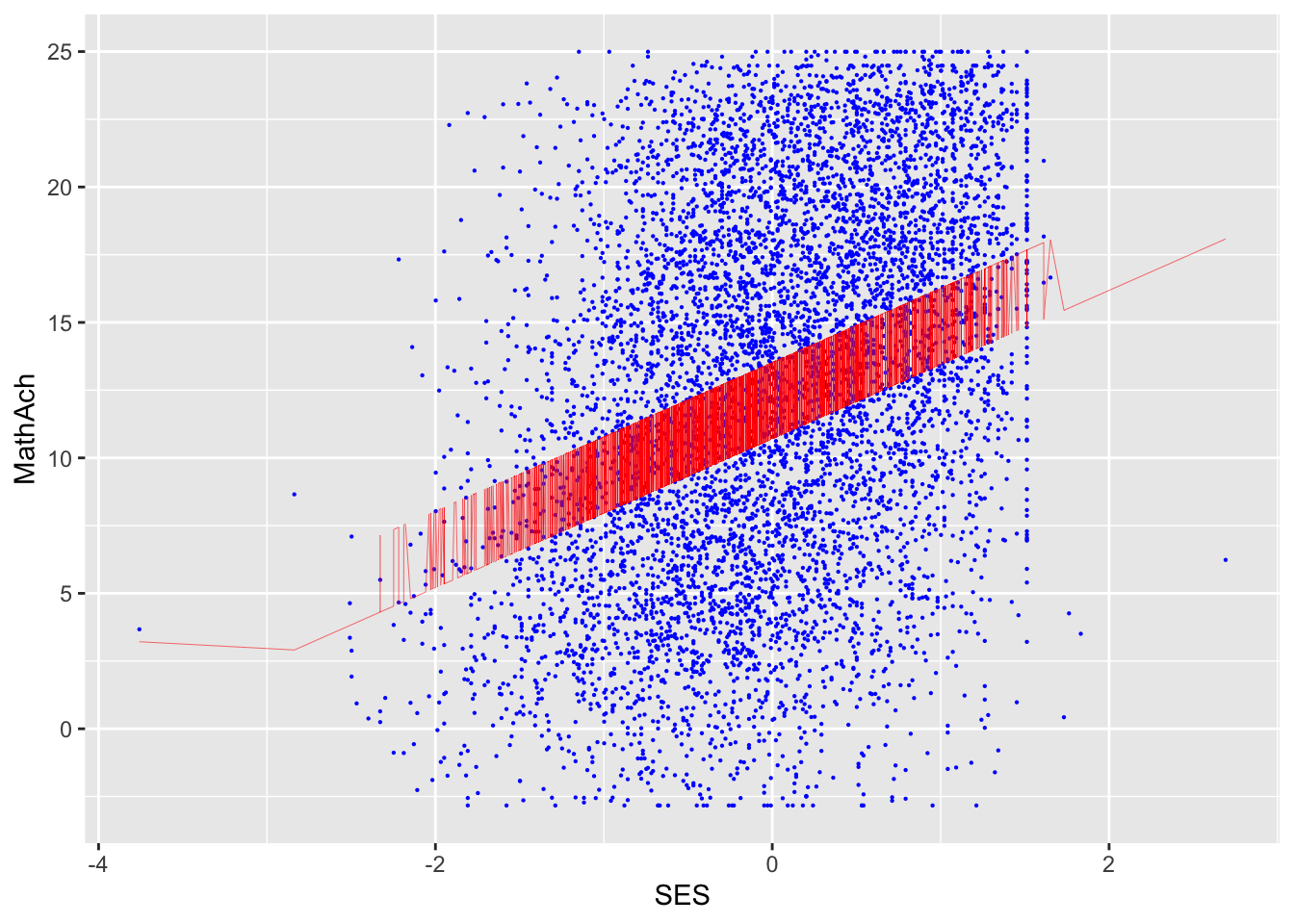
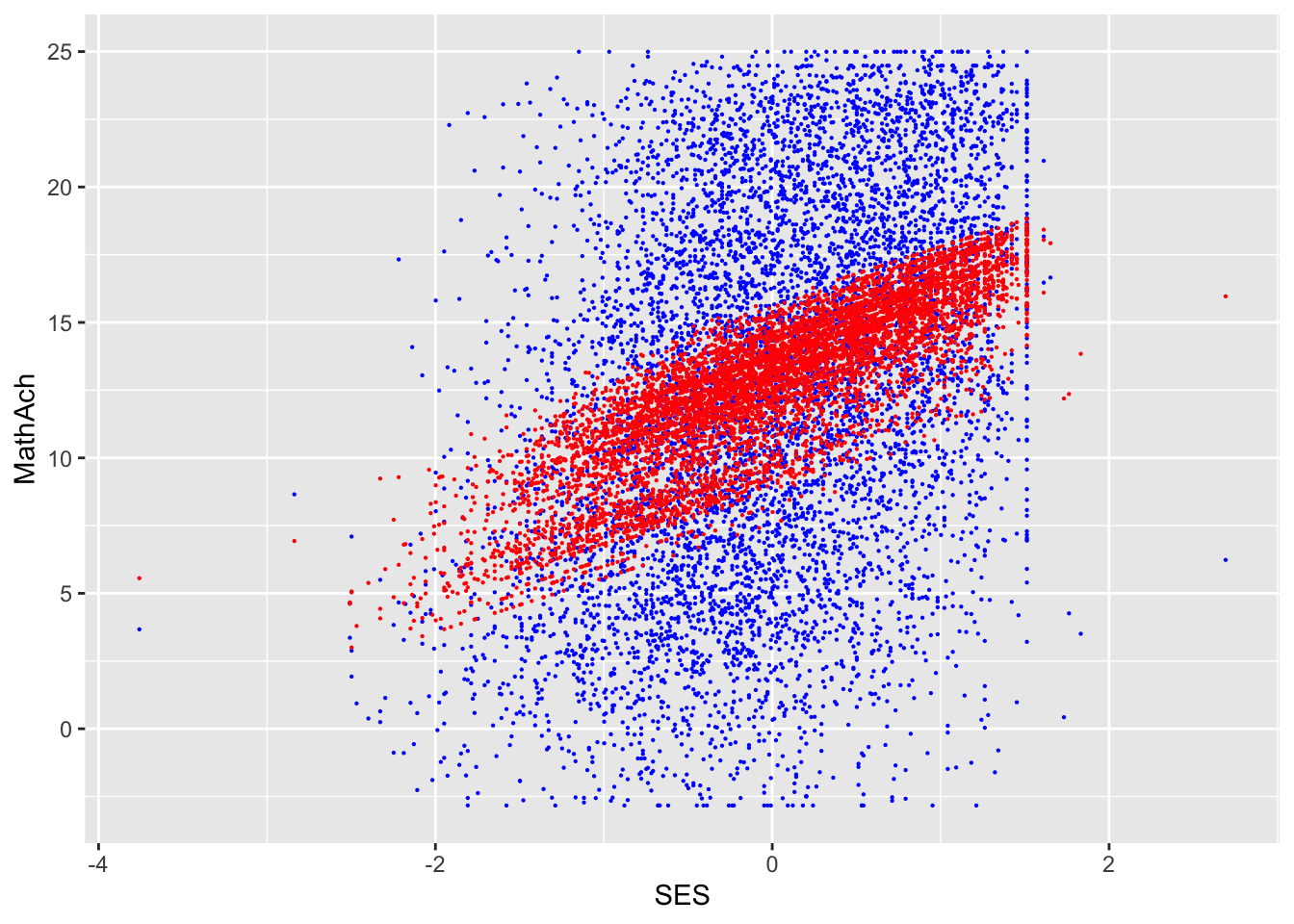
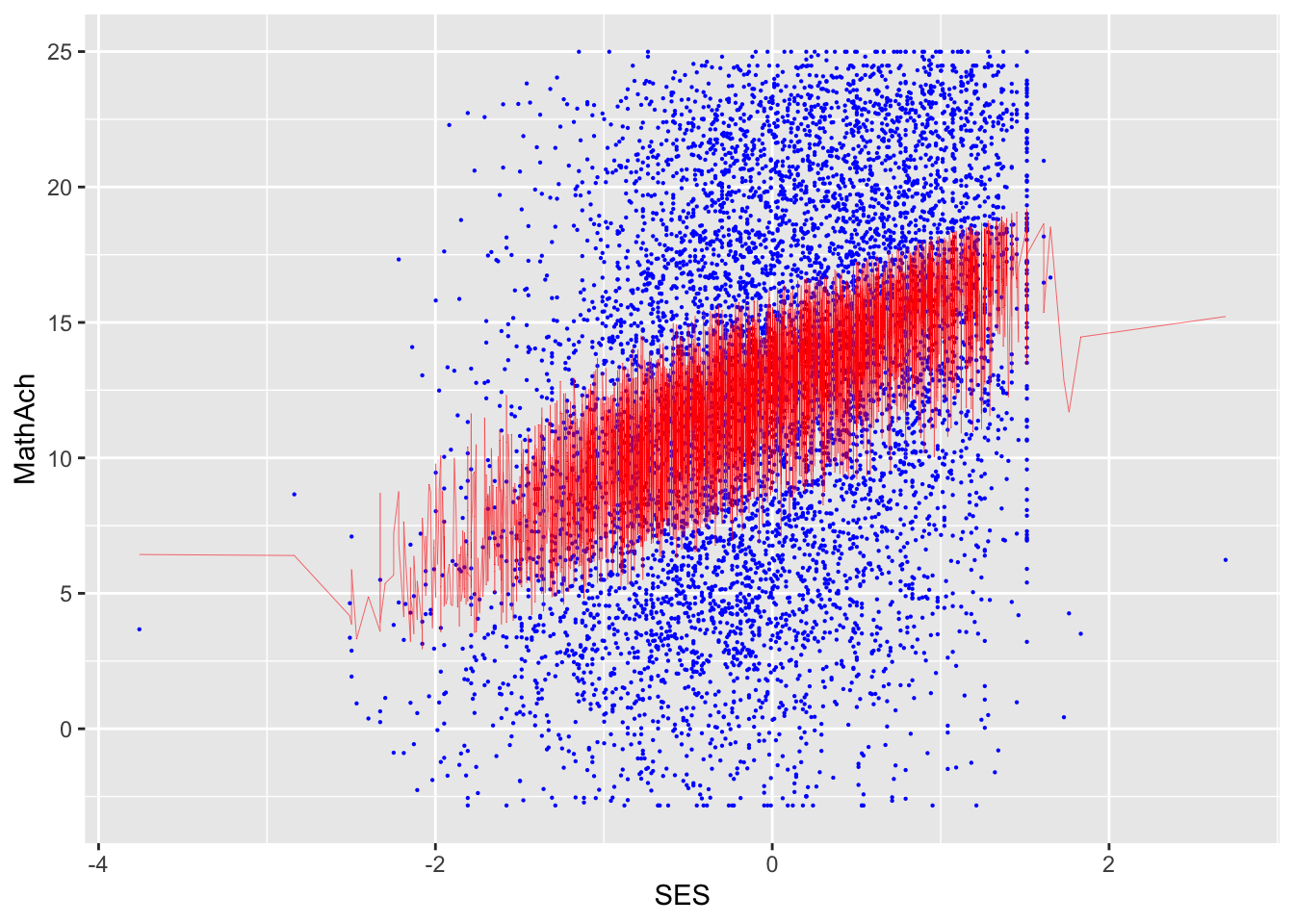
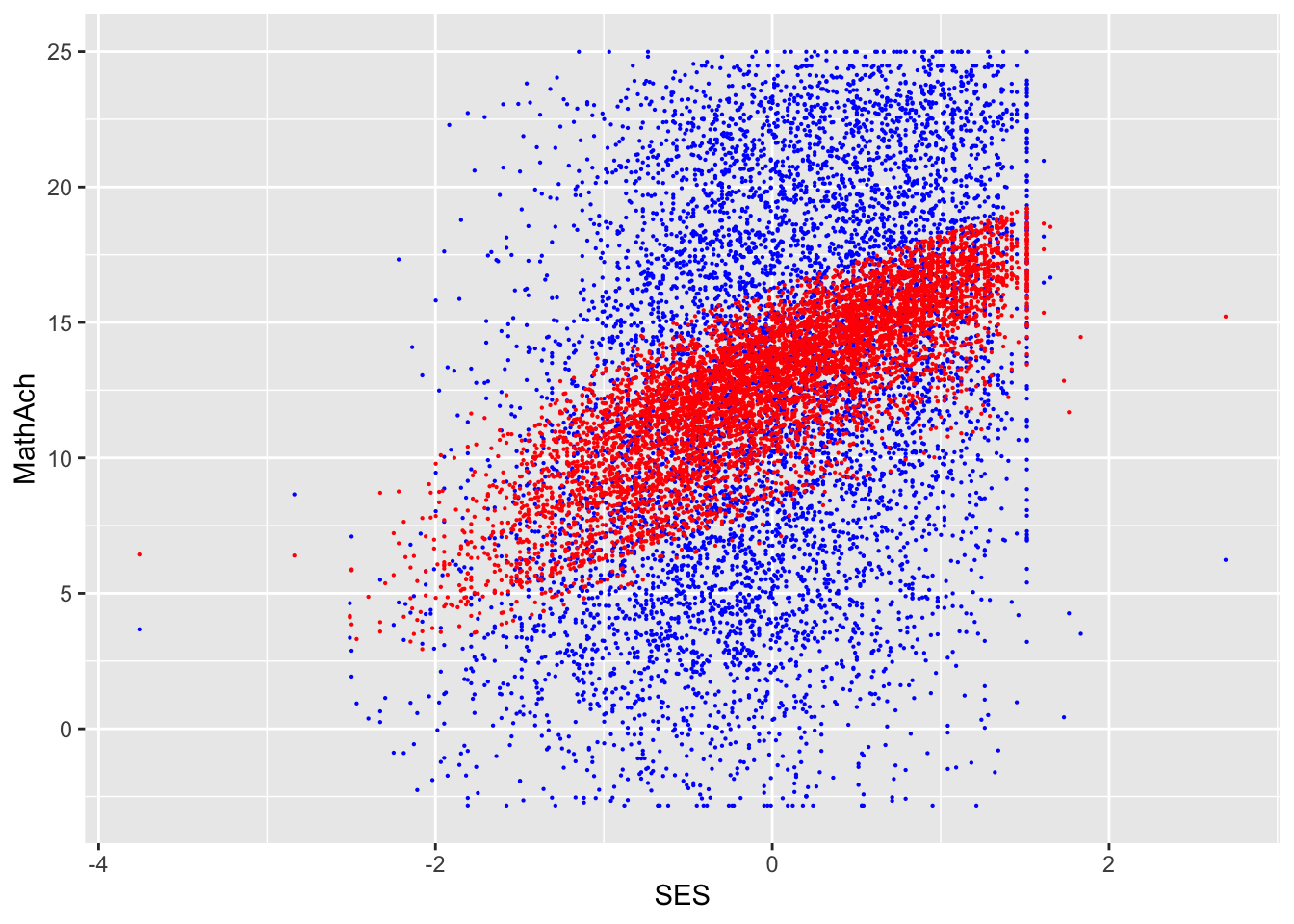
• SES and MEANSES look like distributions centered around 0

• MathAch is centered around ~13 and has -ve scores! Curious how one can attain a negative achievement score in Math: must be somehow a normalized variable.

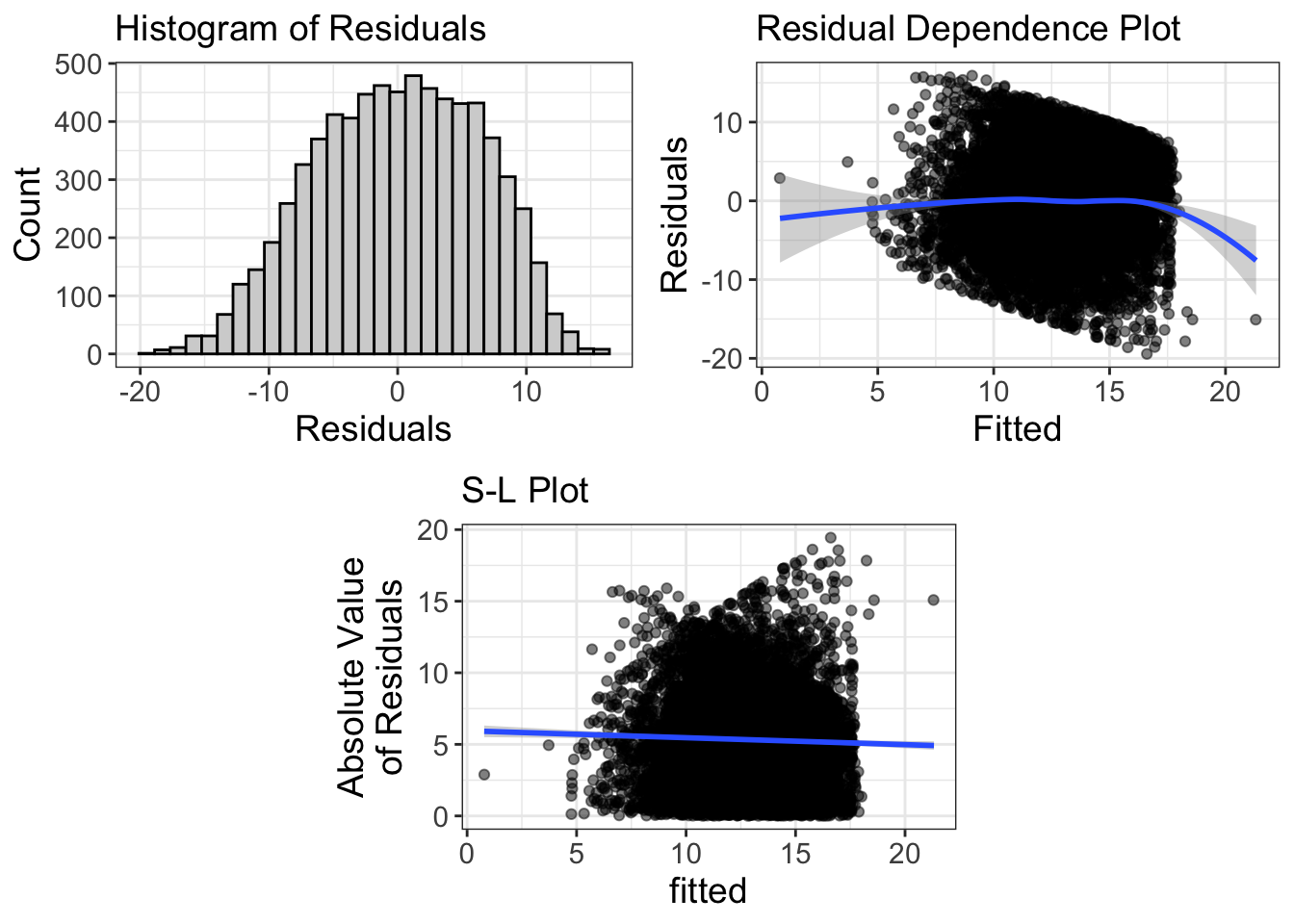
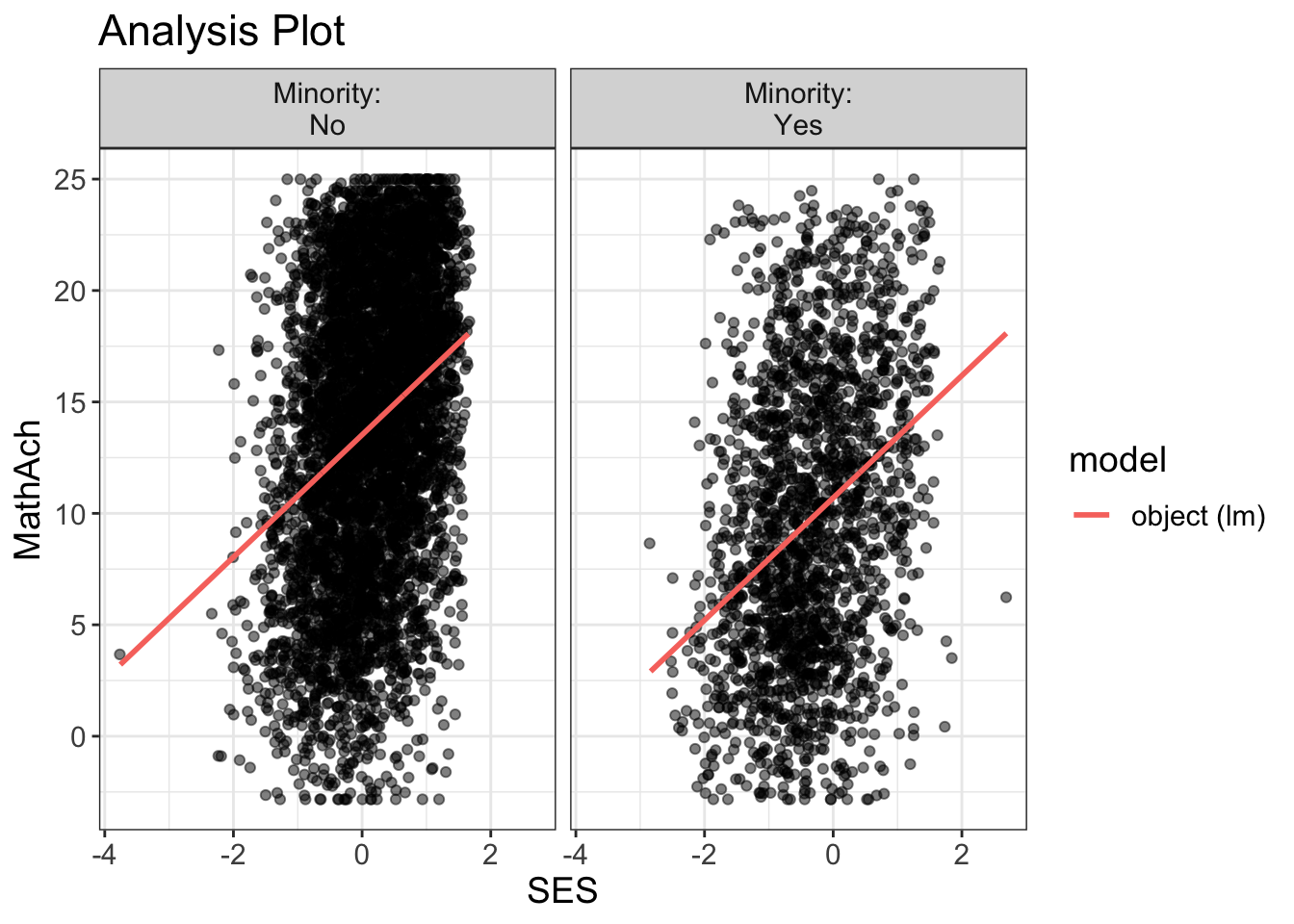
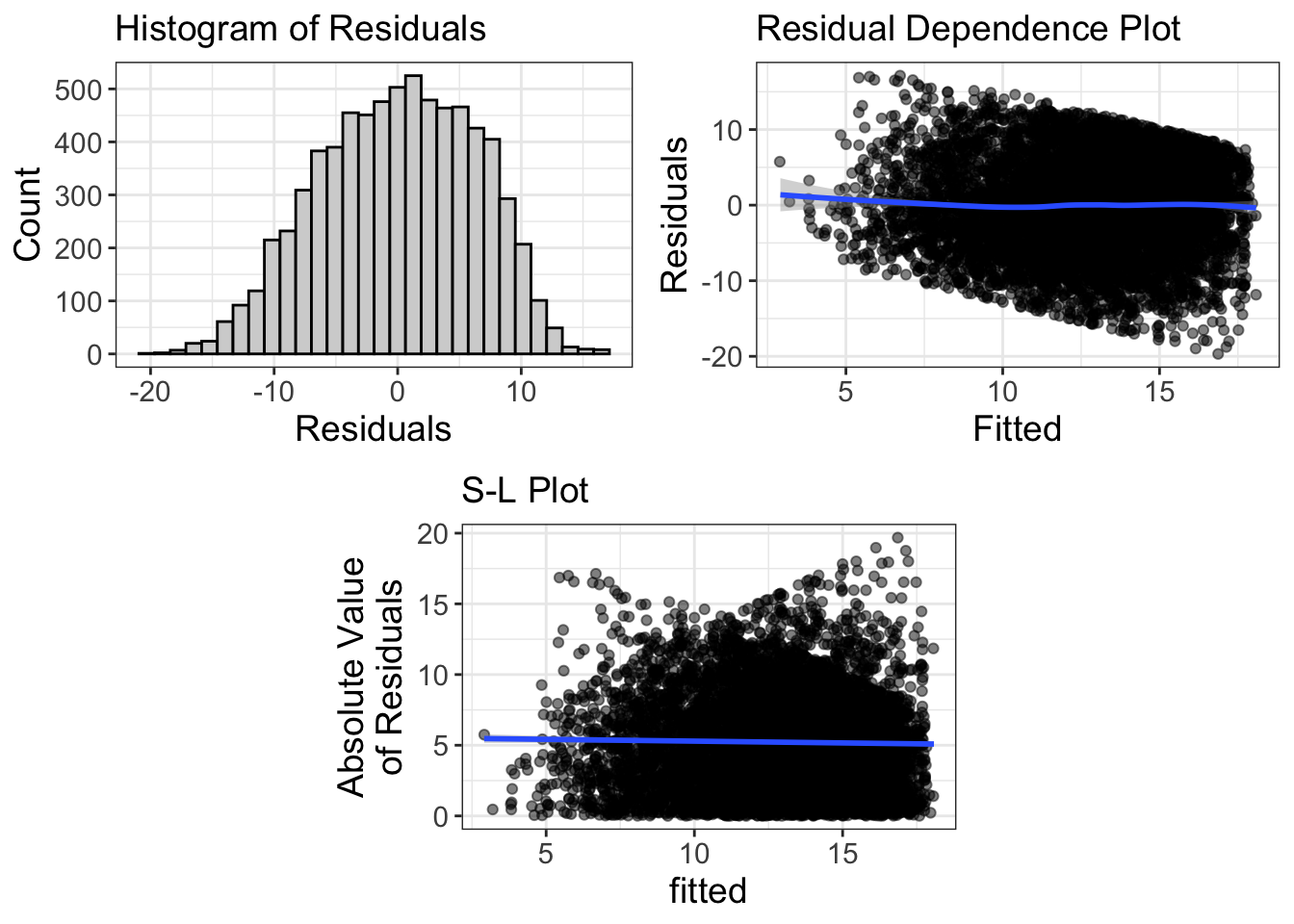
• Do some plots to look more closely at distributions

# plots 
ggplot(math, aes(MathAch)) +
  geom_histogram(binwidth = 0.1)

ggplot(math, aes(SES)) +
  geom_histogram(binwidth = 0.05)

ggplot(math, aes(MEANSES)) +
  geom_histogram(binwidth = 0.01)

Variable Meanings

• SES is Socio-Economic Status or Score?

• MEANSES is presumable the mean of SES that is already calculated for each school ID

• MathAch is achievement in Math?

No predictor model

# no predictor
mod_baseline <- lmer(MathAch~1 + (1|School), data=math)
visualize(mod_baseline, plot = "model", sample = 12)

Coordinate system already present. Adding new coordinate system, which will
replace the existing one.

summary(mod_baseline)

Linear mixed model fit by REML ['lmerMod']
Formula: MathAch ~ 1 + (1 | School)
   Data: math

REML criterion at convergence: 47116.8

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.0631 -0.7539  0.0267  0.7606  2.7426 

Random effects:
 Groups   Name        Variance Std.Dev.
 School   (Intercept)  8.614   2.935   
 Residual             39.148   6.257   
Number of obs: 7185, groups:  School, 160

Fixed effects:
            Estimate Std. Error t value
(Intercept)  12.6370     0.2444   51.71

First model with predictors: fixed and random effects

# SES as fixed and random effect
mod_ses <- lmer(MathAch~SES + (SES|School), data=math)
visualize(mod_ses, plot = "model", sample = 6)

summary(mod_ses)

Linear mixed model fit by REML ['lmerMod']
Formula: MathAch ~ SES + (SES | School)
   Data: math

REML criterion at convergence: 46640.4

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-3.12272 -0.73046  0.02144  0.75610  2.94356 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 School   (Intercept)  4.8287  2.1974        
          SES          0.4129  0.6426   -0.11
 Residual             36.8301  6.0688        
Number of obs: 7185, groups:  School, 160

Fixed effects:
            Estimate Std. Error t value
(Intercept)  12.6650     0.1898   66.71
SES           2.3938     0.1181   20.27

Correlation of Fixed Effects:
    (Intr)
SES -0.045

Comments

Fixed effect is very clear with individual schools being close to parallel to fixed effect

Compare baseline and first model

# compare models
model.comparison(mod_baseline, mod_ses)

refitting model(s) with ML (instead of REML)

$statistics
                  aic      bic bayes.factor      p
mod_baseline 47122.79 47143.43 0.000000e+00 <2e-16
mod_ses      46652.40 46693.68 4.605423e+97       

$predicted_differences
   0%   25%   50%   75%  100% 
0.000 0.514 1.071 1.802 8.991 

$r_squared_change
   Residual (Intercept) 
 0.05921519  0.43943350 

Comments

• Bayes Factor favors mod_ses and great p value

• R^2 change (by using mod_ses that has SES predictor):

  • explains 5.92 % of the residual variance. Difference between fitted models for each cluster (in this case, each school).

  • 43.94 % of variance in intercept (relative to the mod_base that has no predictor - juts the mean of every data point)

• Visualize that….

# see the difference with 3 example schools
compare.fits(MathAch~SES | School, mod_baseline, mod_ses, data = math)

Comments

• Plots are narrow

• sample=n is not observed

A better model? Let’s see

# a better model including Minority?
mod_ses_minority <- lmer(MathAch~SES + Minority + (SES|School), data=math)
visualize(mod_ses_minority, plot = "model", sample = 6)

summary(mod_ses_minority)

Linear mixed model fit by REML ['lmerMod']
Formula: MathAch ~ SES + Minority + (SES | School)
   Data: math

REML criterion at convergence: 46443

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.1742 -0.7243  0.0283  0.7577  3.0047 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 School   (Intercept)  3.9362  1.9840        
          SES          0.3187  0.5645   -0.40
 Residual             35.9967  5.9997        
Number of obs: 7185, groups:  School, 160

Fixed effects:
            Estimate Std. Error t value
(Intercept)  13.5047     0.1827   73.92
SES           2.1326     0.1156   18.44
MinorityYes  -2.9782     0.2081  -14.31

Correlation of Fixed Effects:
            (Intr) SES   
SES         -0.194       
MinorityYes -0.307  0.173

• Compare … to understand “variance explained”
  • We get statistics on variance of
    • Residuals (calculated over all model point deviations from individual group regression lines - random effects)
    • Intercept (fixed effect versus random effects at the intercept)
    • Slopes (comparison of individual group regressions - random effects vs group effects)

# better model?
# compare models
model.comparison(mod_baseline, mod_ses_minority)

refitting model(s) with ML (instead of REML)

$statistics
                      aic      bic  bayes.factor      p
mod_baseline     47122.79 47143.43  0.000000e+00 <2e-16
mod_ses_minority 46457.03 46505.19 3.917437e+138       

$predicted_differences
   0%   25%   50%   75%  100% 
0.000 0.564 1.187 2.028 7.690 

$r_squared_change
   Residual (Intercept) 
 0.08050517  0.54305152 

• Bayes Factor is much better: 3.917437e+138 vs 4.605423e+97

• R^2 change (by using mod_ses_minority that has SES and Minority predictors):

  • explains 8.05 % of the residual variance. Difference between fitted models for each cluster (in this case, each school) vs ~6%

  • 54.31 % of variance in intercept (relative to the mod_base that has no predictor - just the mean of every data point)

• Visualize that….

# see the difference with 3 example schools
compare.fits(MathAch~SES | Minority + School, mod_baseline, mod_ses_minority, data = math)

Compare first and second models

# compare models
model.comparison(mod_ses, mod_ses_minority)

refitting model(s) with ML (instead of REML)

$statistics
                      aic      bic bayes.factor      p
mod_ses          46652.40 46693.68 0.000000e+00 <2e-16
mod_ses_minority 46457.03 46505.19 8.506139e+40       

$predicted_differences
   0%   25%   50%   75%  100% 
0.000 0.206 0.428 0.957 3.183 

$r_squared_change
   Residual (Intercept)         SES 
 0.02263002  0.18484518  0.22830024 

• 2.326 % improvement in residual fit

• 18.48% improvement in intercept variance

• SES unexplained variance reduced by 22.83 %

# see the difference with 3 example schools
compare.fits(MathAch~SES | Minority + School, mod_ses, mod_ses_minority, data = math)

What about a regular linear models

• some additional ggplots will help with understanding variables

# it's a factor
math$School <- as.factor(math$School)

1 Predictor

# SES with Minority colouring
ggplot(math, aes(x=SES, y=MathAch, colour=Minority)) + 
  geom_point(size=0.1) + 
  geom_smooth(method = "lm", formula = 'y ~ x', se = TRUE, color="blue")

# model 1 factor 
lm1 <- lm(MathAch ~ SES, data = math)
summary(lm1)

Call:
lm(formula = MathAch ~ SES, data = math)

Residuals:
     Min       1Q   Median       3Q      Max 
-19.4382  -4.7580   0.2334   5.0649  15.9007 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 12.74740    0.07569  168.42   <2e-16 ***
SES          3.18387    0.09712   32.78   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.416 on 7183 degrees of freedom
Multiple R-squared:  0.1301,    Adjusted R-squared:   0.13 
F-statistic:  1075 on 1 and 7183 DF,  p-value: < 2.2e-16

visualize(lm1, plot="model")

visualize(lm1, plot="residuals")

Comments

• It’s not obvious from the scatter-plot points that SES will be a good predictor - though regression line with SE shows the correlation.

• MinorityYes points can be seen emerging in bottom left - less SES ~ less MathAch

• SES is highly significant though the Adjusted R-squared is small (0.13)

2 Predictors

# Belt and braces: Minority box and violin
ggplot(math, aes(x=Minority, y=MathAch, colour=Minority)) + 
  geom_violin() + 
  geom_jitter(shape=16, position=position_jitter(0.4), size=0.3) +
  geom_boxplot(width=0.1, colour="black") 

# and let's have a look at Sex now we are here
ggplot(math, aes(x=Sex, y=MathAch, colour=Sex)) + 
  geom_violin() + 
  geom_jitter(shape=16, position=position_jitter(0.4), size=0.3) +
  geom_boxplot(width=0.1, colour="black") 

# 2 factors
lm2 <- lm(MathAch ~ SES + Minority, data = math)
summary(lm2)

Call:
lm(formula = MathAch ~ SES + Minority, data = math)

Residuals:
     Min       1Q   Median       3Q      Max 
-19.6824  -4.6338   0.2277   4.9502  17.1271 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 13.52473    0.08822  153.31   <2e-16 ***
SES          2.74398    0.09909   27.69   <2e-16 ***
MinorityYes -2.82912    0.17299  -16.35   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.3 on 7182 degrees of freedom
Multiple R-squared:  0.1614,    Adjusted R-squared:  0.1611 
F-statistic:   691 on 2 and 7182 DF,  p-value: < 2.2e-16

visualize(lm2, plot="model")

visualize(lm2, plot="residuals")

Comments

• Box Violin plot show clearly the effect of Minority

• Median is about 5 points down for Yes

• SES and Minority together are better predictors

• How to visualize a model using 2 or more indepandant variables?

  • look at this nice example plucked from the interweb

# read dataset
df = mtcars

# create multiple linear model
lm_fit <- lm(mpg ~ cyl + hp, data=df)
#summary(lm_fit)

# save predictions of the model in the new data frame 
# together with variable you want to plot against
predicted_df <- data.frame(mpg_pred = predict(lm_fit, df), hp=df$hp)

# this is the predicted line of multiple linear regression
ggplot(data = df, aes(x = mpg, y = hp)) + 
  geom_point(color='blue') +
  geom_line(color='red',data = predicted_df, aes(x=mpg_pred, y=hp))

• And now the same approach for the 2 factor model, lm2:

  • lm2 <- lm(MathAch ~ SES + Minority, data = math)

# save predictions of the model in the new data frame 
# together with variable you want to plot against
predicted_df <- data.frame(MathArc_pred = predict(lm2, math), SES=math$SES)

# this is the predicted line of multiple linear regression
ggplot(data = math, aes(x = SES, y = MathAch)) + 
  geom_point(color='blue',size=0.1) +
  geom_line(color='red',linewidth=0.1, data = predicted_df, aes(x=SES, y=MathArc_pred))

3 Predictors

# interesting 
# what does this mean.. 3 predictors...shows
lm3 <- lm(MathAch ~ SES + Minority + School, data = math)
# summary(lm3)
# undo above comment to go down the hole
#
# Does this mean that the model with SES + Minority is better for some schools?
# TO DO

# 3 predictors
lm3 <- lm(MathAch ~ SES + Minority + MEANSES, data = math)
summary(lm3)

Call:
lm(formula = MathAch ~ SES + Minority + MEANSES, data = math)

Residuals:
     Min       1Q   Median       3Q      Max 
-20.4561  -4.5692   0.1964   4.8371  17.6516 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 13.36822    0.08786  152.16   <2e-16 ***
SES          1.99956    0.11202   17.85   <2e-16 ***
MinorityYes -2.32435    0.17476  -13.30   <2e-16 ***
MEANSES      2.92260    0.21421   13.64   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.22 on 7181 degrees of freedom
Multiple R-squared:  0.1826,    Adjusted R-squared:  0.1822 
F-statistic: 534.6 on 3 and 7181 DF,  p-value: < 2.2e-16

predicted_df <- data.frame(MathArc_pred = predict(lm3, math), SES=math$SES)
# this is the predicted line of multiple linear regression
ggplot(data = math, aes(x = SES, y = MathAch)) + 
  geom_point(color='blue',size=0.1) +
  geom_line(color='red',linewidth=0.1, data = predicted_df, aes(x=SES, y=MathArc_pred))

ggplot(data = math, aes(x = SES, y = MathAch)) + 
  geom_point(color='blue',size=0.1) +
  geom_point(color='red',size=0.1, data = predicted_df, aes(x=SES, y=MathArc_pred))

4 Predictors

# 4 predictors
lm4 <- lm(MathAch ~ SES + Minority + MEANSES + Sex, data = math)
summary(lm4)

Call:
lm(formula = MathAch ~ SES + Minority + MEANSES + Sex, data = math)

Residuals:
     Min       1Q   Median       3Q      Max 
-19.7498  -4.4732   0.2485   4.8209  18.0243 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  12.7503     0.1111 114.772   <2e-16 ***
SES           1.9551     0.1115  17.533   <2e-16 ***
MinorityYes  -2.3410     0.1738 -13.469   <2e-16 ***
MEANSES       2.8675     0.2131  13.455   <2e-16 ***
SexMale       1.3200     0.1466   9.005   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.186 on 7180 degrees of freedom
Multiple R-squared:  0.1917,    Adjusted R-squared:  0.1912 
F-statistic: 425.7 on 4 and 7180 DF,  p-value: < 2.2e-16

predicted_df <- data.frame(MathArc_pred = predict(lm4, math), SES=math$SES)
# this is the predicted line of multiple linear regression
ggplot(data = math, aes(x = SES, y = MathAch)) + 
  geom_point(color='blue',size=0.1) +
  geom_line(color='red',linewidth=0.1, data = predicted_df, aes(x=SES, y=MathArc_pred))

ggplot(data = math, aes(x = SES, y = MathAch)) + 
  geom_point(color='blue',size=0.1) +
  geom_point(color='red',size=0.1, data = predicted_df, aes(x=SES, y=MathArc_pred))

Compare models

# compare standard 1 and 2 predictor models
model.comparison(lm1, lm2)

$statistics
         aic      bic bayes.factor      p   rsq
lm1 47103.94 47124.58 0.000000e+00 <2e-16 0.130
lm2 46843.23 46870.75 1.312994e+55        0.161

$predicted_differences
   0%   25%   50%   75%  100% 
0.051 0.565 0.886 1.472 3.236 

Comments

• lm2 better than lm1

# compare 2 and 3 predictor models
model.comparison(lm2, lm3)

$statistics
         aic      bic bayes.factor      p   rsq
lm2 46843.23 46870.75 0.000000e+00 <2e-16 0.161
lm3 46661.35 46695.75 1.000671e+38        0.183

$predicted_differences
   0%   25%   50%   75%  100% 
0.001 0.348 0.708 1.170 4.025 

Comments

• lm3 better than lm2

# compare 3 and 4 predictor models
model.comparison(lm3, lm4)

$statistics
         aic      bic bayes.factor      p   rsq
lm3 46661.35 46695.75 0.000000e+00 <2e-16 0.183
lm4 46582.66 46623.93 3.934229e+15        0.192

$predicted_differences
   0%   25%   50%   75%  100% 
0.477 0.612 0.655 0.697 0.875 

Comments

• lm4 better than lm3

# compare 1 and 4 predictor models
model.comparison(lm1, lm4)

$statistics
         aic      bic  bayes.factor      p   rsq
lm1 47103.94 47124.58  0.000000e+00 <2e-16 0.130
lm4 46582.66 46623.93 5.169085e+108        0.192

$predicted_differences
   0%   25%   50%   75%  100% 
0.000 0.542 1.159 1.964 6.671 

Comments

• bayes.factor seems to be additive lm1 <- lm2 <- lm3 <-lm4
• lm4 is much better than lm1

# compare the standard 2 predictor model with the MM with 2 predictors 
model.comparison(lm2, mod_ses_minority)

$statistics
                      aic      bic bayes.factor
lm2              46843.23 46870.75 0.000000e+00
mod_ses_minority 46457.03 46505.19 2.402547e+79

$predicted_differences
   0%   25%   50%   75%  100% 
0.000 0.495 1.097 1.965 7.403 

Comments

• MM better than standard 2 predictor variable model?

# compare the standard 2 predictor model with the MM with 2 predictors 
model.comparison(lm4, mod_ses_minority)

$statistics
                      aic      bic bayes.factor
lm4              46582.66 46623.93 0.000000e+00
mod_ses_minority 46457.03 46505.19 6.102683e+25

$predicted_differences
   0%   25%   50%   75%  100% 
0.000 0.511 1.045 1.826 7.019 

Comments

• ..